「論理的思考」は、磨けば磨くほど、どんどん成長していきます。
前回のクイズの解答・解説です。
前回のブログ記事に載せたクイズの「答え」を発表します。
問題編は、こちら(前回のブログ)です。
まずは、第１問です。
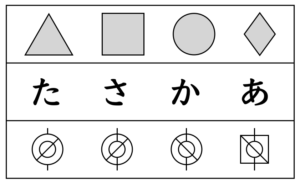
左から順に「正三角形(さんかく)」「正方形(ましかく)」「円(まる)」「ひし形」ですが、
正三角形、正方形、ひし形は「角(チクチク)」や「辺(まっすぐな線)」がある「多角形」の仲間であるのに対して、
円は、角や辺がありません。
算数で使う言葉がわからなくても、「どれが仲間ではない」か分かった新１年生の子も多かったのではないでしょうか。
続いて、第２問です。
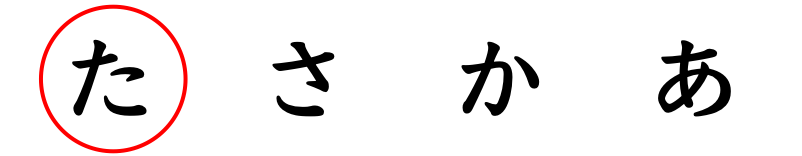
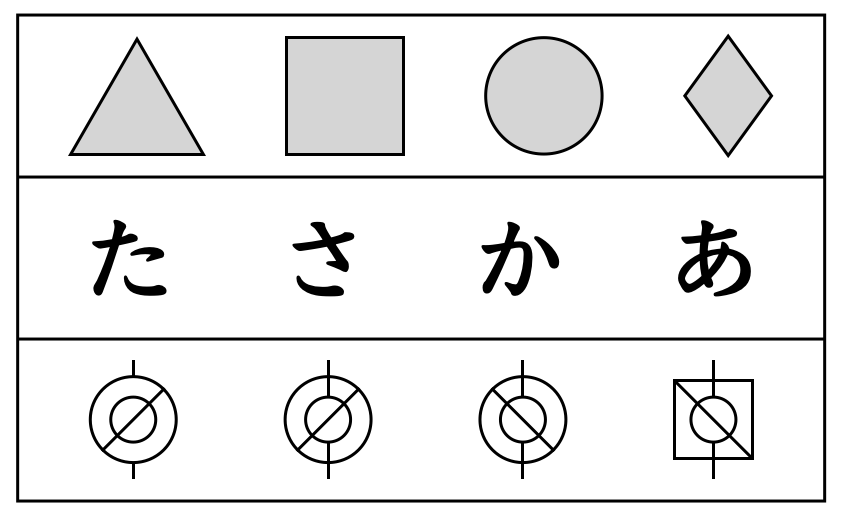
いずれも、「あ段(五十音表の一番上の段)」のひらがなが並んでいるのですが、
「た」のみ、画数が４画です。
(「あ」「か」「さ」の画数は３画です。)
また、この問題については、
先日のアドバンスクラスでも「別解」が出たのでご紹介します。
別解）「あ」だけ、濁点「゛」がついて濁音にならないので仲間はずれ。
これは、出題の際の意図とは異なりましたが、
「仲間ではない」納得の理由があるため、
この別解も「正解」となります。
この「仲間はずれ」の問題ですが、
もしかしたら、他にも「別解」が存在するかもしれません。
ご家庭でクイズに挑戦する際は、
答えを選んだ際に、「それが仲間ではない理由」を、あわせて答えてもらうようにしてください。
仲間集め(分類)について、論理的に考えられることと、
自分の思考を「言語化」できることが、
このクイズの「目的」でもあります。
ここにはない「別解」でも、
お子さまの答えが「納得」の理由であれば、
それも、ぜひ「正解」としてあげてください。
最後に、第３問です。
この問題は、上の２問と比べても、なかなかの「難問」です。
ちょっとした「発想の逆転」が必要です。
とにもかくにも、答えから見ていきましょう。
こちらが「仲間ではない」理由は、
ズバリ、「他の３つには、仲間はずれのところがある」からです。
具体的に、他の３つが、どこが違っているかを赤で示します。
(１番左)…縦の線が大きな円の内側まで伸びていない
(右から2番目)…斜めの線の向きが逆
(１番右)…外側の大きな円が正方形になっている
このように、３つの形は、いずれも
「他の３つとは違う」部分があります。
ですが、左から2番目の形だけは、
どの部分を見ても、「他の２つ(あるいは３つ)と同じ形」しかありません。
仲間はずれがあるのが「仲間」で、
仲間はずれがないのが「仲間はずれ」。
言葉にすると、ますます、ややこしくなってきそうですね。
同じ論理で「仲間はずれ」を探す問題は
「IQテスト」にも存在していますので、
(解けたら、大人でもIQ100〜120くらいになる問題でしょうか。)
これは、「いじわる問題」でもなんでもない、
れっきとした「論理クイズ」です。
そして、少しヒントも出しましたが、
低学年のアドバンス生の中からも正答者が出たのは、「さすが」としか言いようがありません。
こうした「論理」について頭をひねることが、
「算数(数学)的思考」を磨く秘訣でもあります。
また、折に触れて、こうしたクイズも出していこうと思っていますので、
ぜひ、挑戦してみてください。
投稿者プロフィール
最新の投稿
学習教室2024年3月31日前向きな気持ちで、新年度を迎えましょう。
学習教室2023年12月31日2023年の終わりによせて
学童教室2023年8月31日夏休みも終わり、２学期がスタートしてきます。
学童教室2023年8月4日もし、chatGPTに読書感想文を書かせてみたら？
