【解答・解説】図形の等分問題
年末の一大イベント(?)である、クリスマスも終了しました。
皆さんは、どのようなクリスマスをお過ごしでしたでしょうか。
クリスマスについてはさておき、
前回のブログ記事で出題した、図形の等分問題について、解答と解説を発表していきましょう。
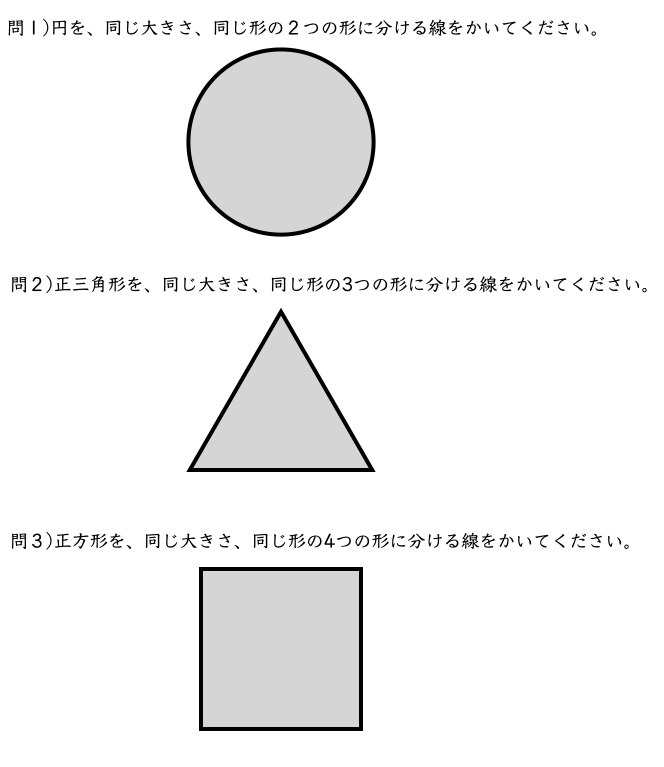
基本的な図形である円(まる)、正三角形(さんかく)、正方形(ましかく)を、同じ大きさ、同じ形に分けるように線をかく、と言うのは、
就学前からお勉強をしてきている年長さんでも、答えを出すことができる問題のはずです。
この問題について、
数ある答えの中から、もっとも多くの方が選ぶであろう「正解」を、まずは発表します。
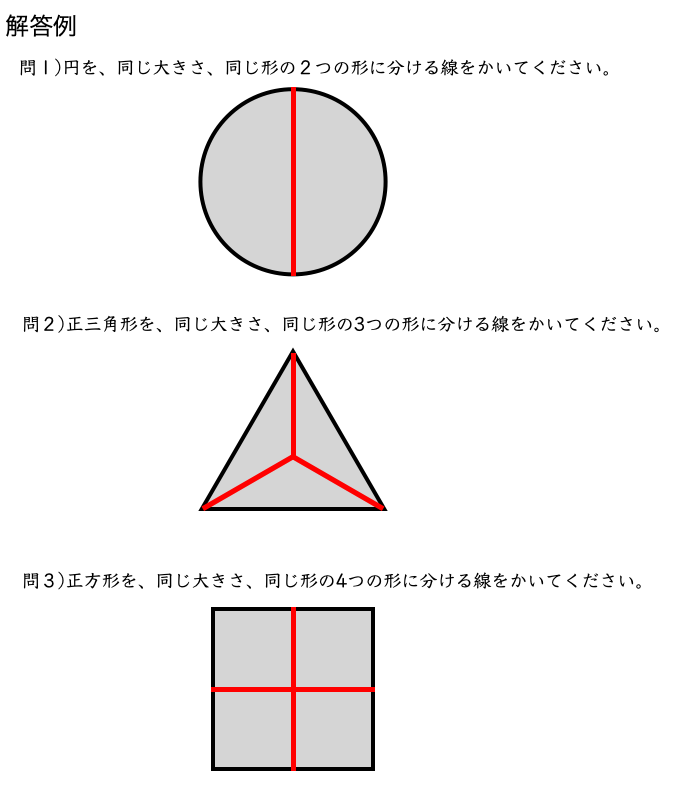
このようにすれば、正解です。
この中では、「三角の３等分」が、少しだけ難しかったかもしれません。
これ以外の、答えを考えた人も、いるかもしれませんので、
別解をいくつかご紹介します。
円(まる)を２つに切る線は、横でも、斜めでも実際は同じです。
そして、正方形(ましかく)の４等分は、さまざまな切り方のパターンが存在します。
これ以外にも、×のマークになるように線を書いて、４つの直角二等辺三角形に分ける方法もありますね。
さて、ここで、
正三角形(さんかく)の別解を見てみてください。
実は、最初の正解も含めて、３つとも、
「三角形の中心(重心)から、120°の角を３つ作るように伸びている３本のまっすぐな線(線分)」によって分けられている、と言うことがわかります。
最初の答えの３本の線の形を基準(0°)としたら、
別解の左側は、それを反時計回りに60°回転させたもの、
別解の右側は、同じく反時計回りに、こちらは90°回転させたものです。
３本の線が重なっているところを中心として、線を回していけば、
(0°≦θ＜120°の範囲に)無数に答えがある、ということになります。
これは、正方形を４等分するときの、直交した２本の線分においても、同じことが言えます。
(２本の線の交点を中心に、0°≦θ＜90°の範囲に無数に答えがあります。)
また、形を等分するのは、必ずしもまっすぐな線である必要はありません。
円の２等分の場合は、
「中心から等しい距離にある2点が、中心から正反対の場所にある」ように
正三角形の３等分は、
「中心から等しい距離にある3点が、どの２点から中心に向かって直線を引いても、その交点の角度が120°となる」ように
正方形の４等分は、
「中心から等しい距離にある4点を結ぶと正方形ができる」ように、
それぞれ、中心から辺まで(あるいは頂点まで)連続した点をかくことで、完成します。
言葉での説明が、あまり上手くできませんでした。
「百聞は一見にしかず」ということで、
実際に、他の別解をご覧ください。
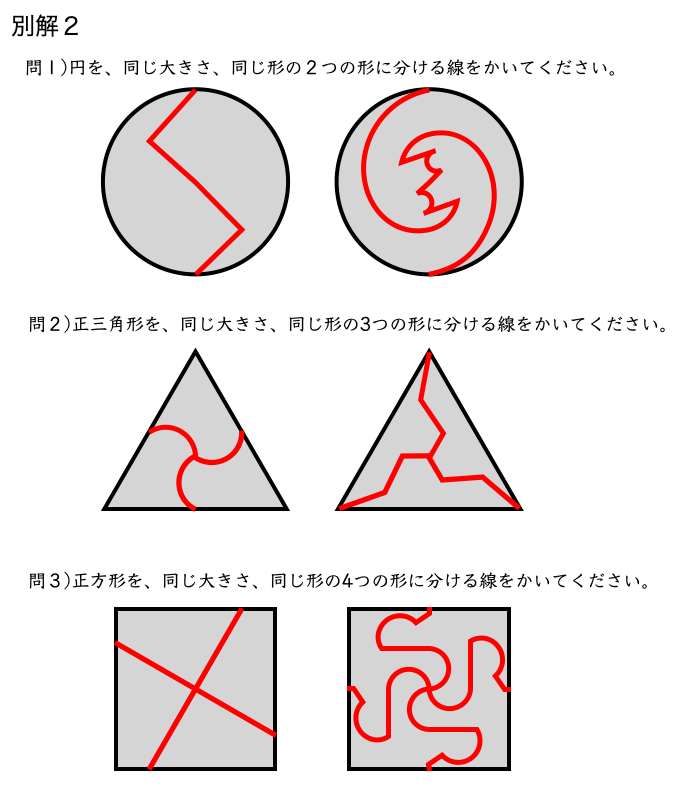
いかがでしたでしょうか。
最後の別解については、
小学生にとっては、なかなかマニアックなレベルになっていますが、
ぜひ、自由に、形を作図してみて、
実際に形を切って、重ね合わせることで、
「形の等分は、無限にあるんだな」ということを、確かめてみてください。
強烈な体験による学びが、
必ずや、図形問題への興味関心の向上につながるはずでしょう。
投稿者プロフィール
最新の投稿
学習教室2024年3月31日前向きな気持ちで、新年度を迎えましょう。
学習教室2023年12月31日2023年の終わりによせて
学童教室2023年8月31日夏休みも終わり、２学期がスタートしてきます。
学童教室2023年8月4日もし、chatGPTに読書感想文を書かせてみたら？
