(小学生高学年以上むけ)前回の分数問題の解答・解説
今回の記事は、
前回のブログで出題した「分数問題」について、
答え合わせと解説をしていきます。
問）□の①②に入る数字(整数)の組み合わせは何通りでしょうか。(①,②)の形ですべての組み合わせをあげましょう。
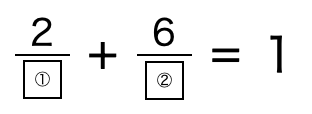
当初の設問の意図としては、
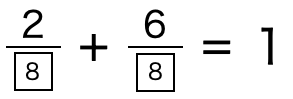
が答えられれば、「小３レベルの分数の学習内容の理解」ができています。
ですが、この問題の□に入る数字の組み合わせは、(①,②)=(8,8)だけではありません。
たとえば、
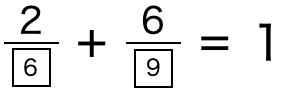
といった数字でも可能です。
（2/6は、１を6個に分けたうちの２つ分なので、1/3と同じで、
同様に6/9は2/3と同じです。)
他にも、①と②の組み合わせはあるでしょうか。
まずは、小学生(高学年)でも理解できる内容で解説をしていきます。
分子が同じで、分母が変わると、分数はどうなるか。
たとえば、左側の「□分の２」について考えてみましょう。
□の中の数が、大きくなると、分数はどうなるでしょうか。
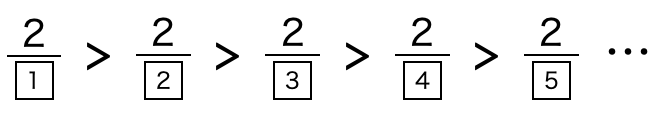
このように、分子が同じ数の時、
分母が大きくなればなるほど、その分数は小さくなります。
（数字だけでイメージが難しい場合は、実際に数直線を使って大きさを比較してみるとわかりやすいです。）
この中で、(「□分の２」と「□分の６」がそれぞれプラスの数となるとすると、)
「□分の２」は、１より小さくなるため、
①の中に入る数は、３より大きくなります。
ですから、①のなかに、３から順番に数を入れて、考えてみましょう。
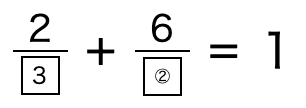
2/3とあわせて１になるのは、1/3なので、
「□分の６」が3分の１となるような②は18。
よって、(①,②)=(3,18)
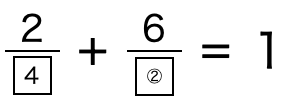
同様に、「□分の６」は2分の１となるので、②は12。
よって(①,②)=(4,12)
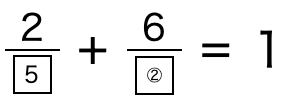
「□分の６」が5分の３となる②は10。
よって(①,②)=(5,10)
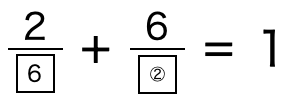
これは、先ほどの例で上がっていました。
(①,②)=(6,9)
次は、順番に考えたら①＝７ですが、
ここで、先にあげた、この式から考えます。
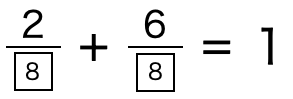
右側の分数は、
ひとつ上の、「9分の６」から、
分母が１つ減って、「8分の６」となっています。
②に入る数字が整数である場合、6/9と6/8の間に入る数はない(8と９の間に整数はないから)ので、
2/6と2/8の間にある2/7と、足して１になる「□分の6」は無い、ということになります。
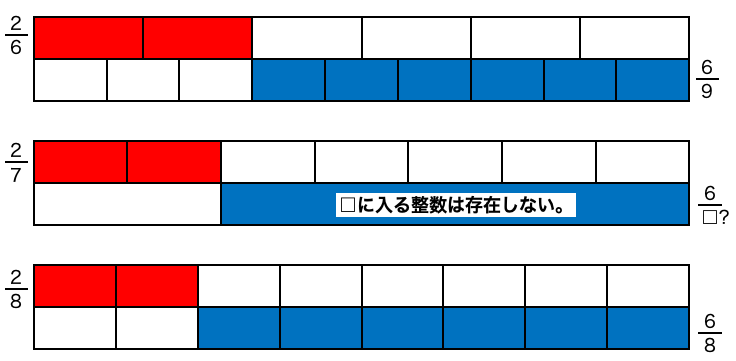
よって、(①,②)=(7,②)となる②はなく、
次は、(①,②)=(8,8)となります。
そのように考えると、以降は、②の数字を順に小さくしていけば答えが分かります。
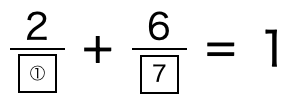
「□分の２」が7分の1となる①は、14です。
よって、(①,②)=(14,7)
そして、②は６以下になると、□分の６が１以上になってしまうので、
②=6とはなりません。
なので、問題の答えとなるのは、以上の６組となります。
答）(①,②)=(3,18),(4,12),(5,10),(6,9),(8,8),(14,7)の６通り
小学生の考え方では、上記の順番で考えて、順番に計算をしながら解いていくことができれば、正解にたどり着くことができたかもしれません。
高学年としても、発展問題の領域と言えるでしょうから、
６通り全てを、順番に見つけ出すことができた人は、
分数の理解がよくできていて、算数力がかなり高いと言えるでしょう。
（ひょっとしたら、大人の方でも、考えることを放棄してしまうような難問かもしれませんね。）
おまけ）数学で考えると……、
小学生の皆様には需要がないですが、
この問題を、数学の考え方で処理すると、このようになります。
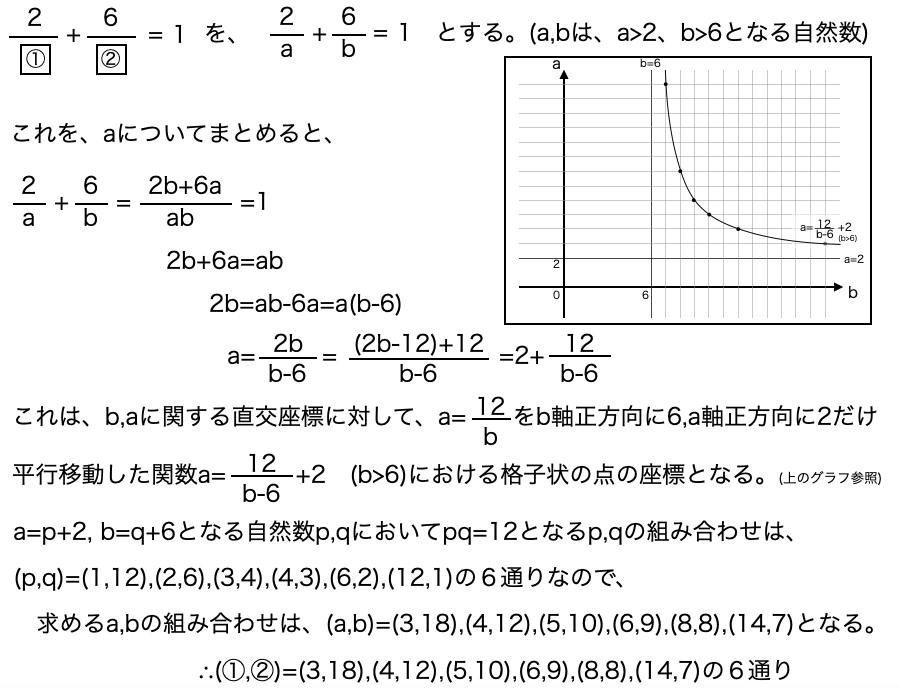
小学生の知識では、答えを、ひとつひとつ見つけ出す必要がありましたが、
中学以降の「数学」の考え方を使えば、
まとめて、①と②の組み合わせを把握することができました。
算数と数学は、
大きくルールが変わるような印象もありますが、
問題を解くための「道具」を集めていく、というスタンスは同じです。
算数の問題も、いろいろな考え方を使いこなせるようになっていくために、
様々な問題を、試行錯誤しながら考えていくことの積み重ねが、力になります。
考え方をマスターした上で、
スムーズに計算をしていく力も必要になっていきますので、
基礎の計算練習にも、繰り返し取り組んで、マスターしていきましょう。
明日は、アドバンスクラスのオンライン教室です。
明日は、発展的な学習についての授業も行います。
（とは言っても、ブログの分数問題と比べたら、簡単ですのでご安心ください。）
皆様と一緒に、
「？」が「！」になる学びの時間を過ごしましょう。
投稿者プロフィール
最新の投稿
学習教室2024年3月31日前向きな気持ちで、新年度を迎えましょう。
学習教室2023年12月31日2023年の終わりによせて
学童教室2023年8月31日夏休みも終わり、２学期がスタートしてきます。
学童教室2023年8月4日もし、chatGPTに読書感想文を書かせてみたら？
