全ての組み合わせを網羅する際は「順番」に気をつける。
先週末も、四ツ谷アドバンスクラスは大盛況でした。
先週末の日曜日のアドバンスクラスは、
新１年生となる年長さん主体のお教室でした。
アドバンスクラスの基本の流れに沿って、
集中して90分の学習に取り組みました。
冷静に考えると、すごいことなのですが、
小学生のアドバンス生に混じって、
まだ、小学校に入学していないお子さまが10名。
全員が、途中で集中力が切れることなく、最後まで学習に取り組めました。
就学前にして、すでに、学習の基盤が整っている状態。
これは、明らかに、就学前の学習習慣の「成功」を意味しています。
もちろん、細かい学習の一つひとつに「知らない」「わからない」「できない」はあるかもしれません。
むしろ、「あって当然」とも言えるでしょう。
それらは、しかしながら、
これからの学習の積み重ねで、いくらでも「できる」に変わっていきます。
これからの成長も、ますます楽しみですね。
日々、ご家庭でも学習を積み重ねていきましょう。
さて、先日の「一筆書きクイズ」の解答について紹介します。
一筆書きのルールは「奇点から始まり奇点に終わる」だったわけですが、
では、その中で、「決まった描き出しから一筆書きで描くことができる方法は、何通りあるか」について考えてみる、というのが、
最新の出題でした。
この後の描き方は、全部で何通りでしょうか。
前回のブログでは、
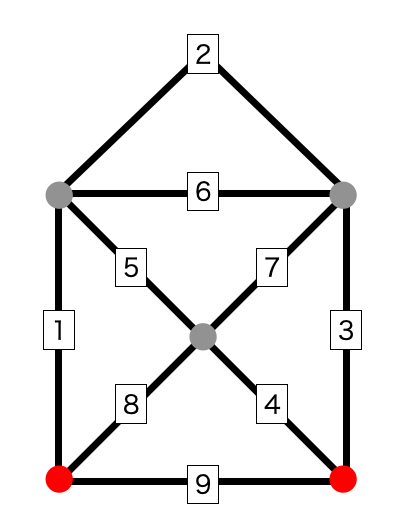
「それぞれの辺に番号をつける」ことによって、
描き方の順番を数字で示す方法を紹介しました。
今回は、実際に漏れがないよう、全てのパターンを挙げていきましょう。
「何通り」かを確認する問題における「お約束」
今回の出題のように、「何通りか」を答える問題で、
少し時間はかかるけど確実に正解できるのは
「全てのパターンを漏れなく挙げる」方法です。
大切なのは、その際に
「漏れがない」で全てのパターンを挙げ切ることです。
そのためには、
パターンを挙げていく「順番」に工夫が必要です。
上記の「番号」をふった形で、それぞれの辺を通る順番を挙げていく時、
「なるべく、小さい番号から進むものから、順に挙げていく」
というルールを設定するようにします。
具体的には、
設問で指定されている（１,２, 、と進んだ後の道は、
「３」「６」「７」と道が分かれていますが、
この中で、一番小さい「３」の方向に進んだ後の順番から、考えていくようにします。
「３」の後は、「４」か「９」です。
なので、小さい方の「４」から進みます。
次は、「５」「７」「８」なので、「５」を選択します。
すると、残った道は「６７８９」の１通りしかないので、
「１,２,３,４,５」と進んだ後の通り方は１通りです。
これを、(１,２,３,４,５６７８９)と書くことにします。
次は、「１,２,３,４,７」を考えます。
これも、その後は「６５８９」と１通りに決まります。
これは、(１,２,３,４,７６５８９)です。
そして、「１,２,３,４,８」と進むと、「５６７」の辺を通ることができなくなるので、この進み方では一筆書きはできません。
よって、「１,２,３,４」と進んだ後の描き方は、
(１,２,３,４,５６７８９)
(１,２,３,４,７６５８９)
の２通りとなります。
次は、「１,２,３,９」を考えます。
その次は、「８」しかあり得ないので、「１,２,３,９８」となります。
その後、「５」か「７」に道が分かれ、
(１,２,３,９８,５６７４)と
(１,２,３,９８,７６５４)の２通りが一筆書きできる方法となります。
よって、「１,２,３」と進んだ後の書き方が、
(１,２,３,４,５６７８９)
(１,２,３,４,７６５８９)
(１,２,３,９８,５６７４)
(１,２,３,９８,７６５４)
の４通りとわかりました。
同様に、「１,２,６」も調べていきます。
そうすると、全てのパターンは、
(１,２,６５,４,３７８９)
(１,２,６５,４,９８７３)
(１,２,６５,７３,４９８)
(１,２,６５,７３,８９４)
(１,２,６５,８９,３７４)
(１,２,６５,８９,４７３)
の６通りとなります。
最後に「１,２,７」について調べます。
この後のパターンは、
(１,２,７,４,３６５８９)
(１,２,７,４,９８５６３)
(１,２,７,５６３,４８９)
(１,２,７,５６３,９８４)
(１,２,７,８９,３６５４)
(１,２,７,８９,４５６３)
の計６通りです。
以上から、
「１,２」と進んだ後の描き方は、
4+6+6=16通りあることがわかりました。
全ての通り方は、以下の通りです。
(１,２,３,４,５６７８９)
(１,２,３,４,７６５８９)
(１,２,３,９８,５６７４)
(１,２,３,９８,７６５４)
(１,２,６５,４,３７８９)
(１,２,６５,４,９８７３)
(１,２,６５,７３,４９８)
(１,２,６５,７３,８９４)
(１,２,６５,８９,３７４)
(１,２,６５,８９,４７３)
(１,２,７,４,３６５８９)
(１,２,７,４,９８５６３)
(１,２,７,５６３,４８９)
(１,２,７,５６３,９８４)
(１,２,７,８９,３６５４)
(１,２,７,８９,４５６３)
これを、さらに手前の分岐についても調べていきます。
さて、今回の問題は、
「１,２」と進んだ後のパターンだけでしたから、まだまだでしたが、
「１」の道からスタートした後の書き方は、
「１,２」の他に、「１,５」「１,６」の２通りがあります。
さらに、最初の描き出しが左下の奇点からだったとしても、
「１」の他に、「８」「９」の描き出しがあります。
全ての「描き方」を網羅しようとなると、
とても多くなりそうなことがわかりますね。
気になる方は、ぜひ、じっくり数字を挙げていってみてください。
後日、ブログ上でも正解を発表したいと考えています。
(よりシンプルに正解を出せる方法もありますが、それも、また後日。)
投稿者プロフィール
最新の投稿
学習教室2024年3月31日前向きな気持ちで、新年度を迎えましょう。
学習教室2023年12月31日2023年の終わりによせて
学童教室2023年8月31日夏休みも終わり、２学期がスタートしてきます。
学童教室2023年8月4日もし、chatGPTに読書感想文を書かせてみたら？
