お年玉クイズの「解答」「解説」と、「おかわりクイズ」です。
三連休も終わりました。
みなさんは、充実の連休を過ごせましたでしょうか。
日曜日のアドバンスクラス生の皆さんとは、
連休のちょうど真ん中に、お教室でご一緒しましたね。
学校がない休みの日こそ、
普段は取り組めないような、じっくり考える問題に取り組んだという人もいることでしょう。
前回の「お年玉クイズ」の解答例と解説です。
前回のブログで紹介した、
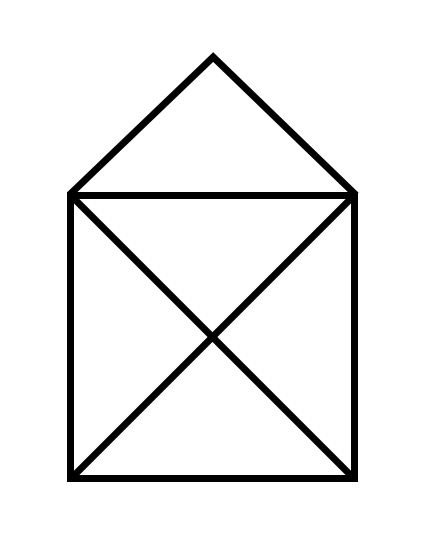
「一筆書きクイズ」について、
その解答の例を紹介します。
「一筆書きクイズ」の詳細はこちらから(前のブログ記事にジャンプします。)
一筆書きクイズの「解答例」
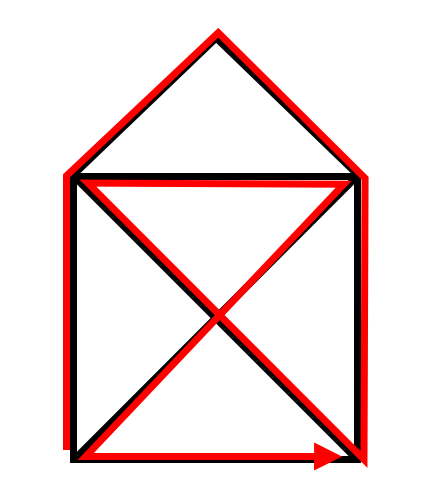
このような矢印の順番で描くと、一筆書きで描くことができます。
これ以外にも、
たくさんの「別解」が存在しますが、
全ての正解を並べてみると、
そこには、共通点が存在します。
それは、必ず、
「形の下にある片方の角から描き始めて、下のもう片方の角で描き終わる」
ということです。
(上の「解答例」では、左下から描き始めて、右下で描き終わっています。)
これは、それぞれの「角(頂点)」から出ている線の数に秘密があります。
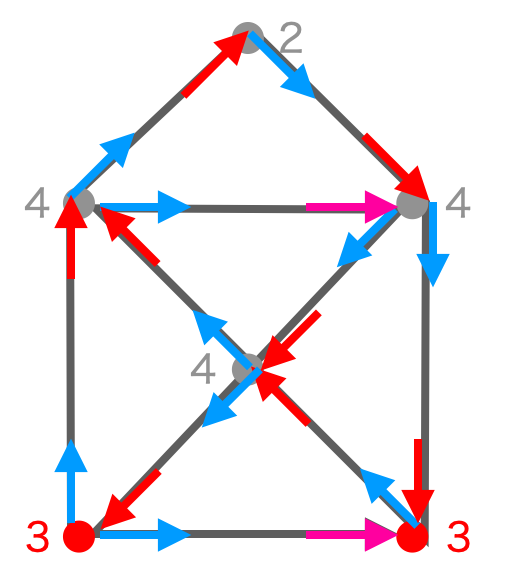
それぞれの角(頂点)から出ている線の数を数えると、下の図のようになります。
このように、下の２つの角(頂点)だけが、そこから出ている線の数が奇数(２で割り切れない数)で、
残りの角から出ている線は、全て偶数(２で割り切れる数)です。
一筆書きをする際には、
必ず、この奇数の線が出ている点(＝奇点)から描き始め、
もうひとつの奇点で描き終わるようにする必要があります。
その理由を考えてみましょう。
それぞれの頂点には、
「その点から出発して書き出される線」と、
「その点に到着するように書かれる線」があるわけですが、
書いている途中でたどり着く点は、
必ず、「到着する線」と「出発する線」の数が同じになります。
唯一、描き始めの点だけ、
「出発する線(図でいう青線)」が1本多く
描き終わりの点だけ、
「到着する線(図でいう赤線)」が1本多いため、
２で割り切れない(＝奇数)線が点に集まっている、ということになります。
ちなみに、
どのような形も、必ず奇点の数は偶数個あります。
奇点が0個の形(＝全ての頂点から出る線の数が偶数)は、どこから描き始めても一筆書きをすることができます。
奇点が4個以上の形は、一筆書きをすることができません。
そんなお約束を知ると、
ある形が「一筆書きできるかどうか」について、
試し書きをしなくとも、ほぼ即座に、判断することができるようになります。
そして、いざ、一筆書きできる形を描こうとする場合も、
迷うことなく、片方の奇点から書き出せば、
確実に、形を書くことができるようになります。
お年玉クイズの「おかわり」です。
さて、
ここからは、ブログを読んでくれている高学年の皆さんと、
特に腕に覚えのある低学年のアドバンス生の皆さんに向けた、追加のクイズです。
今回の一筆書きクイズは、
たくさんの「正解」があることを実感している人も多いと思います。
では、
その「正解」は、
何通りあるでしょうか。
全ての正解を出す前に、
図の赤丸からスタートして、矢印のように描き進めた「後」の、残りの正解のパターンが何通りあるか、考えてみてください。
それができた！という人は、
「全部の正解」が何通りあるかを考えてみても、良いでしょう。
(おそらく、全部の正解を求めるのは、中学受験クラスの難易度かと思います。
実際の入試にこの問題が出たら、解答を躊躇するレベルです。
他に解いてない問題があったら、そちらに先に当たっていきたくなるかもしれません。)
投稿者プロフィール
最新の投稿
学習教室2024年3月31日前向きな気持ちで、新年度を迎えましょう。
学習教室2023年12月31日2023年の終わりによせて
学童教室2023年8月31日夏休みも終わり、２学期がスタートしてきます。
学童教室2023年8月4日もし、chatGPTに読書感想文を書かせてみたら？
